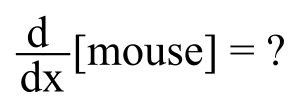Derivative of a mouse

What's the derivative of a mouse? You can take the derivative of a math function, but a mouse isn't a function.

Initial unsolved equation

Possible solutions

There are a number of methods for taking derivatives. One of these is the power rule, which states that the derivative of xⁿ is nx^n-1. How can we apply this to the mouse? The expression "mouse" does not contain any variables, which means it must be a constant and its derivative is 0. However, mice are surely not constants, since they change as time passes.

The power rule only applies to polynomials, so perhaps we need to find a different rule. There are various rules for finding derivatives of other types of functions, such as exponentials; however, a mouse is not any kind of function at all, so none of these will work. (Verify this carefully.)

Derivatives can also be taken with logarithms. However, to use this method we would need to know what the logarithm of a mouse was, and that is another problem entirely.

Mice are solid three-dimensional figures, so they must have slopes. Perhaps the surface of a mouse could be modeled with one or more functions, whose derivatives could then be taken. On the other hand, mice move around a lot and sometimes become larger and/or smaller, and there is more to them than their surfaces, so this could prove to be an impossible task.

Limit definition

As a last resort, we can use the limit definition:

$\lim _{h\rightarrow 0}{\frac {mouse+h-mouse}{h}}$

$=\lim _{h\rightarrow 0}{\frac {h}{h}}$

$={\frac {0}{0}}$

The rapture will be a really good trip.

This tells us that the derivative of a mouse is zero divided by zero. You can't divide by zero, and dividing zero by zero is even worse. It's not even infinity. It's everything and nothing at the same time. It's the end of the world. This was predicted in the Book of Revelations. There is a passage usually interpreted as meaning that everyone will fall down a garish rainbow vortex, and this is obviously connected to dividing by zero because it's all symbolic. The rapture will occur when the date is equal to zero divided by zero. The mark of the beast will take the appearance of a horizontal line between two circles, signifying that doing math wrong means pledging allegiance to Satan. Pay attention in class, kids... or else.

L'Hopital's rule

But wait: when the limit evaluates to 0/0, we can use L'Hopital's rule — that is, take the limit of the derivative of the numerator over the derivative of the denominator. However, the derivative of the denominator is 0, and the numerator includes the expression "mouse" whose derivative we were trying to determine in the first place. In short, it reduces to a previously unsolved problem.

It's mice all the way down.

See also

• Finding the integral of a mouse, which is similar, in that, due to the way integration works, you probably end up with many more mice than you started with. Unfortunately, they're all cut into pieces, and will be dinner for your cat.